1. 流体力学的散逸
惑星大気の散逸は、惑星の初期進化を考える上で非常に重要な問題である。そのためこれまでも、巨大天体衝突に伴う大気の力学的散逸に関する研究 や、太陽のEUV加熱による大気の熱的散逸(流体力学的散逸)、太陽風による荷電粒子の熱的・非熱的散逸に関する研究など、多くの研究が精力的になされて きた(例えば[1], [2])。本研究では、散逸規模が非常に大きく、惑星大気の進化、特に初期進化において重要な役割を果たしたと考えられる流体力学的散逸を扱う。
流体力学的散逸(hydrodynamic escape)とは、静水圧平衡が破れた場合に起こる惑星大気の散逸過程である。惑星大気が全体として大きな運動エネルギーを持ち、惑星の重力を振り切っ て散逸するため、俗に「大気の流出」とも表現される。このうち特に水素の流体力学的散逸、およびそれに引きずられる形でのより重い元素の散逸は、地球の初 期大気問題、希ガス同位体分別問題、あるいは金星の水散逸問題などを解く上で重要な散逸過程である。実際に、流体力学的散逸による大気散逸過程に伴い、地 球・金星・火星の表層環境の違いが作られたことも示唆されている[3]。さらに近年の系外惑星の大気観測に伴い、ホットジュピターやスーパーアースからの 大気散逸も重要な研究テーマになってきている。
しかし、流体力学的散逸の理論解を求めることは容易ではない。古くは80年代から解析的な手法による計算がなされてきたが[4]、音速で特異点を 取るため、音速を超える速度の解を正確に求めることができなかった。また、等温大気やポリトロープ大気を仮定しないと解析解が求まらないため、現実的な問 題への適用は難しいのが現状であった。一方、数値計算による研究も最近になって始められたが[5]、大気成分が複数の場合についての数値計算は未だに実現 されておらず、非常に限定的な問題しか扱えていないのが現状であった。
そこで本研究では、汎用的な計算コードを得ることを目的に、複数成分の大気の流体力学的散逸を解くための計算コードを開発した。そしてその計算コードを金星大気の2つの問題に適用し、初期金星大気に関する新しい知見を得た。
2. 数値計算
複数種の大気成分間の相互作用を考慮した、多相流体1次元時間発展オイラー方程式[6]を解いた。各成分は衝突と熱拡散により運動量を交換し合 い、軽分子が重分子を加速(重分子が軽分子を減速)するシステムになっている。多成分大気の散逸における基本的な考え方は、大気成分中で最も軽いH2が流 体力学的に散逸する際に他の重い分子を加速することで、他の分子を一緒に散逸させるというものである。
大気散逸のエネルギー源としては、太陽EUV(極端紫外線)による上層大気の加熱を考えている。大気加熱の効果を正確に求めるために、太陽の進化 を考慮して太陽系の年代に応じた太陽EUVの値を与えている(図1)[7]。またその分配は、大気成分の各高度での密度や幾何学的な体積、吸収断面積を考 慮に入れて計算した。ちなみに、現在の太陽では紫外線が弱く、惑星大気の流体力学的散逸はほとんど観測されていない。しかし、強い紫外線を出していた若い 太陽(図1)のもとでは、金星や地球の初期大気において大規模な大気の流体力学的散逸が起きていた可能性が考えられる。
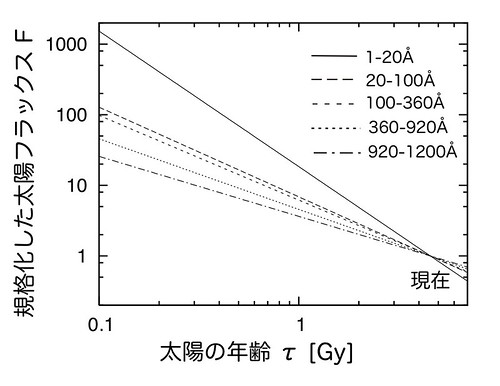
図1: 各波長ごとの、惑星が太陽から受け取るエネルギーフラックスの時間変化。全て現在の値で規格化してある。
数値計算にはセミ・ラグランジュ法を用い、移流項はCIP法[8]により、非移流項は差分法により解いた。CIP法とは、移流計算を行う際に値だ けではなく傾き(微分値)も移流させて数値拡散を小さくする計算法で、大きな密度変化を持つ系の流体方程式を滑らかに解くために開発された。本研究では CIP法を用いることで、亜音速〜遷音速〜超音速まで安定に解を求めることに成功した。また、等温大気やポリトロープ大気の場合に数値解が解析解と一致す ることも確認され、これにより、初めて複数成分の大気の流体力学的散逸を数値的に計算することが可能となった。この計算コードの汎用性は高く、今後は惑星 大気散逸に関する問題を独占的に解くことが可能である。
3. 初期金星大気の散逸
本章では、開発した数値計算コードを用いて多成分大気の流体力学的散逸を計算することで、2つの金星大気問題の解決を図る。
3.1. 金星表面からの水の散逸
3.1.1. 未解決の問題
現在金星上に海は存在しない。しかし過去の研究から、金星の表層には過去に海が存在したことが示唆されている。金星大気中のD/H比(水素と重水 素の存在比)が地球の100倍ほどあることが観測からわかっており[9]、以前は最低でも現在の100倍の水蒸気が存在していたことがわかる。金星表層に 存在した海は、太陽光度の上昇とともに金星が暴走温室状態に入ることで全て蒸発・解離(H2O → H2 + O)し、軽い水素は流体力学的散逸によって宇宙空間に散逸したと考えられている[10]。
ここで問題となるのは、流体力学的散逸で直接散逸できない酸素の行方である。酸素の消費法としてはいくつかの可能性が過去に提案されてきたが、未 だ決定打は無い。地球海洋と等量程度の酸素を金星表面の酸化によって消費するためには、現在の地球よりも大きなテクトニクス活動(惑星表層の更新)を45 億間にわたって続ける必要がある[11]。一方、大気中で酸素を消費するには、COなどの還元的気体が大量に必要となる。いずれの場合も、水が分解して発 生する大量の酸素を全て消費するには、量的に難しいかもしれない。
そこで本研究では、水素の流体力学的散逸に伴う酸素の散逸を考えた。すなわち、軽い水素が散逸する際により重い酸素を引きずって一緒に散逸する可能性を検討した。
3.1.2. 計算結果
流体力学的散逸による水蒸気大気の散逸を計算した。境界条件として、均一圏界面を高度100kmと仮定し、温度を330Kで固定した。ここで均一 圏界面の高度を変えて計算しても、以下で得られた結果は定性的には変わらない。また、海の蒸発・解離に伴い発生する酸素は、O2ではなくOとして散逸する と仮定した。O2は十分に短い時間でOに光解離することがわかっており、酸素が散逸する際の最終状態として単原子Oを選ぶのは妥当である[10]。
図2に、均一圏界面での水素の数密度と太陽系の年代(すなわち太陽EUVの値;図1)を変化させた場合の、水素の散逸フラックスの変化を示す。均 一圏界面での水素の数密度が大きいほど、また太陽系の年代が若いほど、水素の散逸フラックスが大きいことがわかる。また、これらのパラメータの変化に伴 い、水素の散逸フラックスが桁で変化していることもわかる。金星からH2Oが散逸した時期についてはわかっていないので、以下では太陽系の年代を1Gyに 固定して、均一圏界面での水素の数密度をパラメータに計算を行った場合について議論する。
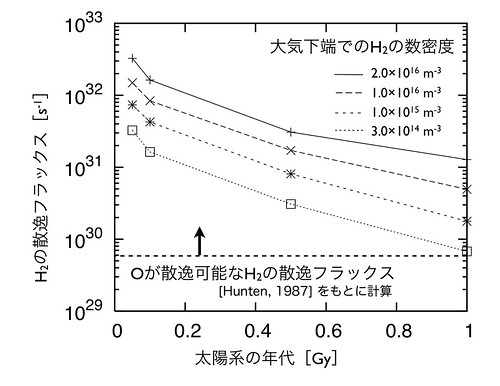
図2: パラメータの変化に伴う水素の散逸フラックスの変化。酸素が散逸可能な水素の散逸フラックスの下限値[12]も図中に示してある。
海の蒸発・解離(H2O → H2 + O)に伴い、均一圏界面でH2 : O = 1 : 1となっている状況を考える。図3に、均一圏界面での水素の数密度を変化させた場合の、水素と酸素の散逸フラックスの変化を示す。均一圏界面での水素の数 密度が1.8×10^16[m-3]以上では、十分な深さの大気まで太陽のEUV加熱が効かないため、水素の流体力学的散逸によって酸素を散逸させること はできない。それ以下の数密度では、水素の流体力学的散逸によって酸素を散逸することが可能であるが、均一圏界面での水素の数密度がさらに減少し 3.0×10^14[m-3]を下回ると、水素の散逸フラックスが十分に大きくならず、酸素を引きずって散逸させることは不可能となる。以上の結果は、太 陽系の年代を変化させても定性的には同様である。
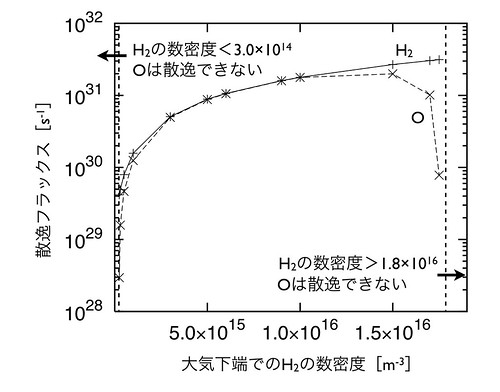
図3: H2 : O = 1 : 1の場合の水素、および酸素の散逸フラックス。太陽系の年代は1Gy。プロットされていない領域では、水素は散逸するが酸素は散逸しない。
図3において、酸素が散逸できないパラメータ範囲では水素のみが散逸するため、相対的に酸素の割合は上昇する。そこで次に、均一圏界面での水素と 酸素の数密度の比を変えた場合を考える。H2 : O = 1 : 1, 1 : 1.1, 1 : 1.5, 1 : 2の状況で、それぞれの場合の酸素の散逸フラックスを計算した結果を図4に示す。酸素の比率が上昇するにつれ、酸素の散逸フラックスが減少し、また酸素が 散逸できるパラメータ範囲も小さくなっていることがわかる。
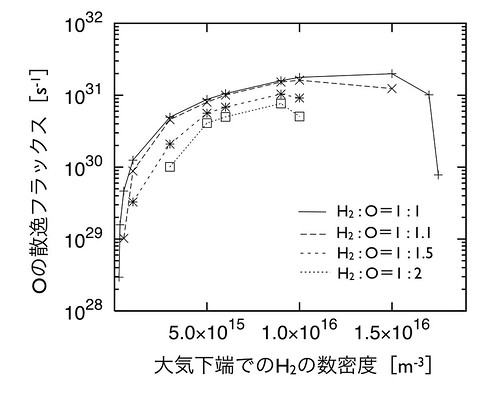
図4: H2 : O = 1 : 1, 1 : 1.1, 1 : 1.5, 1 : 2の場合の酸素の散逸フラックス。太陽系の年代は1Gy。水素の散逸フラックスは示していない。プロットされていない領域では、水素は散逸するが酸素は散逸しない。
3.1.3. 議論
図3を見ると、ほとんどのパラメータ範囲において水素の方が酸素よりも散逸量が大きいため、大気中の酸素の割合は必ず上昇する傾向にあることがわ かる。一方、大気中の酸素の割合が増えると酸素の散逸フラックスは減少し(図4)、さらに酸素の割合は増加することになる。以上より、酸素は必ず大気中に 溜まっていき、流体力学的散逸によって金星の酸素を全て散逸させることは非常に難しいことが結論される。ただし、ある限られたパラメータ範囲(図3では、 均一圏界面での水素の数密度が1.0×10^16[m-3]程度)では、水素と酸素は同量の散逸フラックスを持って散逸することができる。均一圏界面にお いてこの数密度を長期間保持することができれば、流体力学的散逸によって金星の酸素を散逸させることは可能かもしれない。
さて、流体力学的散逸以外に酸素を散逸させる方法として、イオン化した酸素の非熱的な散逸も考えられる。初期金星に磁場が無く、太陽の活動度が長 期間にわたって平均的な太陽型星よりも大きければ、地球海洋と等量程度の酸素を散逸できる可能性がある[13]。しかし非熱的な散逸については未だ不確定 な要素が多く、定量的な議論のためにはさらなる研究の進展を待つ必要があろう。
ところで、上で述べたように大気中に酸素が溜まり酸素分圧が上がり過ぎると、水解離の逆反応である水生成(H2 + O → H2O)が起きる可能性がある。こうなるともはやH2Oそのものを散逸させることが不可能となる。この逆反応の可能性について調べることも、金星からの水 の消失を考える上で重要な研究課題である。
最後に、O/ H2比が1未満の場合について述べておく。金星形成直後の状況を考えると、海の蒸発・解離によって発生した水素以外にも、もともと周囲の太陽系星雲ガスか ら捕獲した水素も大気中に存在しており、金星大気のO/ H2比が1より小さい可能性がある。この場合には、水素の散逸フラックスはより大きくなるため酸素が散逸しやすくなり、酸素に対して十分な量の水素が存在 すれば酸素の全散逸が可能となることが期待される。ただし、金星大気中の水素の割合は、金星大気の進化履歴や海の蒸発の年代などに依存するため、その決定 は容易ではない。今後は、酸素を全散逸させるのに必要な条件を求めることで、逆に金星の大気や海の進化に制約を加えることも行いたい。
3.2. 金星大気中の希ガス存在度の説明
3.2.1. 未解決の問題
金星大気において、Neが太陽組成比より小さくArの存在度が異常に大きいことがわかっている(図5)[14]。その他の希ガスの同位対比などと も照らし合わせると、金星大気からはNeのみが選択的に質量分別を受けたように見える。この希ガス存在度を説明するためのアイデアとして、太陽組成大気か ら希ガスを捕獲した後に散逸によって軽いNeのみを失ったというモデルが提案されている[2]。
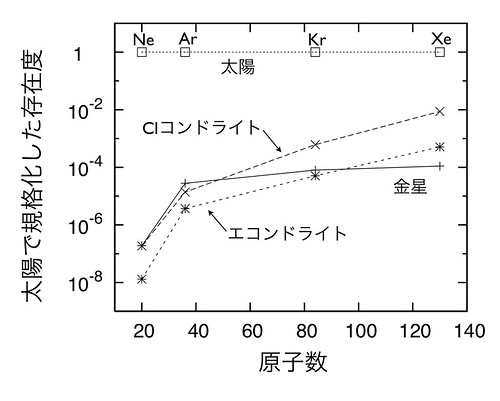
図5: 太陽組成(太陽組成ガス中の存在度)で規格化した金星大気、隕石に含まれる希ガスの存在度。
そこでまず、水素の流体力学的散逸によって各希ガスを散逸させるために必要な水素の散逸フラックスを見積もった(図6)。図6より、NeとArは ほぼ同程度の水素の散逸フラックスで、ともに散逸を開始することがわかる。すなわち、単純な質量分別でNeのみを選択的にArより多く散逸させるのは難し いと思われる。
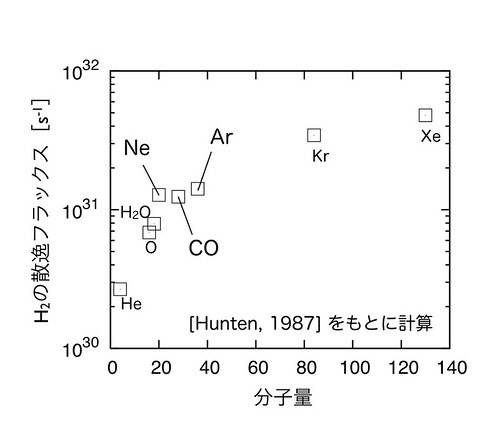
図6: 水素の流体力学的散逸によって各分子を散逸させるために必要な水素の散逸フラックス。
一方このNe/Ar分別について、COの回転スペクトル線による大気の冷却効果を考慮することで、Neのみが散逸可能な温度が自律的に実現される 可能性が示唆されている[6]。図6より、COはNeとほぼ同程度の水素の散逸フラックスで散逸を開始するが、Arを散逸させるのに必要な水素の散逸フ ラックスはそれよりほんのわずかに大きい。NeとCOが散逸を始め上空に上がると、COの冷却効果によって大気が冷やされるため、大気温度が下がり水素の 散逸フラックスが下がる。よって、COが存在することで、NeとCOは散逸するがArは散逸しないという際どい水素の散逸フラックスが、自律的な温度調整 によって得られるのではないかと考えるわけである。
そこで本研究では、希ガスにCOを加えた多成分大気の流体力学的散逸を、CO冷却の効果[15]も考慮に入れて計算し、Ne/Ar分別の可能性について検討した。
3.2.2. 計算結果
太陽系の年代、各大気成分の均一圏界面での数密度を様々に変化させた場合の、NeとArの散逸フラックスの比を計算した結果を表1に示す。ほとん どの場合でNe/Ar分別は実現できていないが、いくつかの特徴的なケースにおいてはNe/Ar分別が実現できる可能性がある。
表1: 太陽系の年代(τ)と各大気成分の均一圏界面での数密度(n)を変化させたときの、NeとArの散逸フラックスの比(F_AR/F_NE )。ただしここで、△: Ne、Arともにほぼ同量が散逸する、▽: Ne、Arともに散逸しない。

Ne/Ar分別が実現できている特徴的なケースについて、均一圏界面でのCOの数密度をパラメータに、NeとArのそれぞれの散逸フラックスを計 算した結果を図7に示す。COが増加するにつれ、冷却効果が強まり大気の温度が下がることで、水素およびそれにひきずられるNe、Arの散逸フラックスが 減少していく。COが水素と同程度の数密度で存在していれば、CO冷却によりNe/Ar分別が最大で1桁分ほど可能であることが分かる。
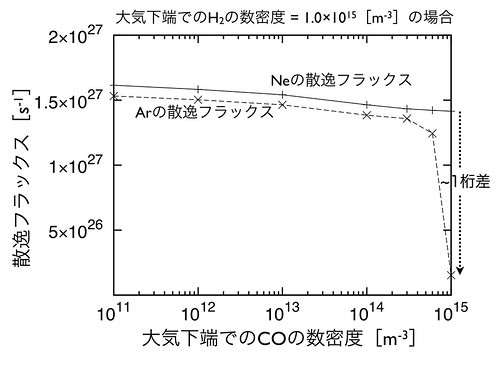
図7: 均一圏界面でのCOの数密度を変化させたときの、NeとArの散逸フラックスの変化。太陽系の年代を0.1Gy、均一圏界面での水素の数密度を1.0×10^15[m-3]に固定した場合。
3.2.3. 議論
先行研究で提案されていたように、COの冷却効果を考慮することで、流体力学的散逸によるNeとArの散逸分別を定性的には実現することが可能で あることがわかった。しかし定量的には、最大で1桁程度の分別では現在の金星の過剰なAr量は説明できず、結局原始大気の流体力学的散逸のみによって現在 の金星大気中のNeとArの存在度を説明することは難しいように思われる[14]。また大気の時間進化を考えると、NeとともにCOもほぼ等量が散逸して いくため、時間とともに大気中のCOの存在度は減少していき、Ne/Ar分別はさらに難しくなることが予想される。
ところでNe/Ar分別の程度を大きくする可能性としては、H2Oによる上層大気の冷却も考えられる。しかしH2O冷却の効果を正確に計算するこ とは容易ではない。そこで、簡単な近似を用いてH2O冷却の効率を見積もった結果[10]、H2O冷却の方がCO冷却よりも数倍程度大きな冷却率を持つこ とがわかった。これは、金星大気中にCOとともに適量のH2Oが含まれることで、Ne/Ar分別を実現するための適当な水素の散逸フラックスが得られる可 能性を示唆している。今後はH2O冷却に関するより詳細な見積もりを行うことが、金星大気中のNe/Ar問題を議論する上で重要な研究課題となるかもしれ ない。
最後に、金星大気の材料物質がそもそもNe/Ar分別を受けたものであった可能性についても述べておく。このような材料物質として、太陽風が打ち 込まれた微惑星[16]、あるいは低温で凝縮した彗星[17]などが過去に提案されている。これらの物質の存在や正確な組成は未だよくわかっていないが、 金星大気が複数の起源と進化の組み合わせによって、現在の組成を持つようになった可能性も考えておくべきであろう。
4. まとめ
開発した多成分流体力学的散逸の数値計算コードを、初期金星大気についての2つの問題に適用した。その結果、金星からの水の散逸、金星大気の Ne/Ar分別のいずれにおいても、流体力学的散逸のみで説明することは比較的難しいことが示された。ただし一方で、これらの問題に対して解決可能な条件 や可能性についても示唆が与えられている。また今後行う必要がある研究課題についても、前章で議論したとおりその方向性を示すことができた。
ところで、本研究では上の2つの問題を独立に解いているが、実際には水の散逸と希ガス分別の時期は重なっていた可能性がある。また、大気中の各分 子の数密度についてはパラメータとして計算をしているが、その量や成分比については、大気の材料物質および進化過程に強く依存する。今後は、惑星(惑星大 気)の進化履歴を考慮に入れた上で、これらの問題について再度考察していく必要があるだろう。
【参考文献】
[1] Genda, H. and Y. Abe, 2005, Nature 433, 842.
[2] Shizgal, B. D. and G. G. Arkos, 1996, Rev. Geophys. 34, 483.
[3] Pepin, R. O., 2006, EPSL 252, 1.
[4] Sekiya, M. et al., 1980, EPSL 50, 197.
[5] Tian, F. et al., 2005, ApJ, 621, 1049.
[6] Zahnle, K. J. and J. F. Kasting, 1986, Icarus 68, 462.
[7] Ribas, I. et al., 2005, ApJ 622, 680.
[8] Yabe, T. et al., 2001, J. Comput. Phys. 169, 556.
[9] de Bergh, C. et al., 1991, Science 251, 547.
[10] Kasting, J. F. and J. B. Pollack, 1983, Icarus 53, 479.
[11] Lewis, J. S. and R. G. Prinn, 1984, Planets and Their Atmospheres (Sao Paulo: Academic Press).
[12] Hunten, D. M. et al., 1987, Icarus 69, 532.
[13] Kulikov, Y. N. et al., 2006, Planet. Space Sci. 54, 1425.
[14] Pepin, R. O., 1991, Icarus 92, 2.
[15] Tielens, A. G. G. M. and D. Hollenbach, 1985, ApJ 291, 722.
[16] Sasaki, S., 1991, Icarus 91, 29.
[17] Owen, T. et al., 1992, Nature 358, 43.


Leave a Reply